Cik tālu jūs varat redzēt meteoru?
>Es saņemu e -pastu.
Lielākā daļa uzdod dažāda veida jautājumus, uz kuriem lielākā daļa ir diezgan vienkārša atbilde (patiesībā uz daudz ko varētu atbildēt, meklējot googlē, ar mājienu). Bet dažreiz man rodas jautājums, uz kuru ir grūtāk atbildēt, vai pat tāds, par kuru esmu aizdomājies par sevi, bet nekad neesmu sapratis.
Tāpēc es biju diezgan ieintriģēts, kad saņēmu jautājumu no sliktā lasītāja Dīna Lūisa par meteoriem. Perseīdu meteoru lietus laikā 2018. gadā viņš bija prom no ģimenes, un to šķīra aptuveni 1000 kilometru. Ja viņš redzēja meteoru, vai bija iespējams, ka viņi varētu redzēt to pašu no tālākas atrašanās vietas?
Īsā atbilde ir: jā! Garā atbilde ir… matemātika. Forša, jautra matemātika.
Un, redzot, kā, publicējot šo rakstu, šovakar 2018. gada ikgadējās Geminid meteoru lietus virsotnes, es domāju, ka ir pareizi to izdomāt.
Avārijas kursa astronomija: meteori, meteoroīdi un meteorīti, ak, mans!
Ja Zeme būtu pilnīgi plakana, tad principā jūs varētu redzēt meteoru līdz pat jebkurai Zemes malai. Kamēr jūs atrodaties virs zemes, pat tīnīte, tad jūsu redzes līnija sasniedz katru jūsu pusē esošās planētas kvadrātcentimetru, tāpēc katrs meteors ir redzams visiem. Patiesībā gaiss nav pilnīgi caurspīdīgs, tāpēc zināmā attālumā jūs skatāties tik daudz netīrumu, ka neko neredzat.
Tomēr Zeme nav plakana. Nopietni! Tas ir apaļš. Un atmosfēra to ieskauj kā čaumalu, augumā kļūstot plānākai un galu galā izlīdzinoties; šis augstums ir atkarīgs no jūsu telpas definīcijas. Tomēr mēs varam mazliet krāpties, jo zinām zinātni: tādi meteori kā dušas mēdz sadedzināt aptuveni 100 kilometrus virs zemes. Šis augstums ir atkarīgs no daudzām lietām, ieskaitot to, cik liels meteoroīdi (cietie starpplanētu gružu fragmenti, kas riņķo kosmosā) ir, cik ātri tie pārvietojas, kādā leņķī tie nonāk atmosfērā utt. Bet sauksim to par 100 km.
Tuvākais meteors jums var būt, ja atrodaties tieši zem tā, un tad tas atrodas 100 km taisni uz augšu (jūsu zenītā). Ja tas sadeg tālāk no zenīta, tad tam jābūt tālāk no jums. Vistālāk jūs varat redzēt meteoru, un tas ir saprātīgi, tāpēc, ja tas atrodas tieši pie horizonta.
Tā ģeometrija izskatās šādi (piezīme: NAV mērogā):
ko nozīmē 111 eņģeļu skaitļi
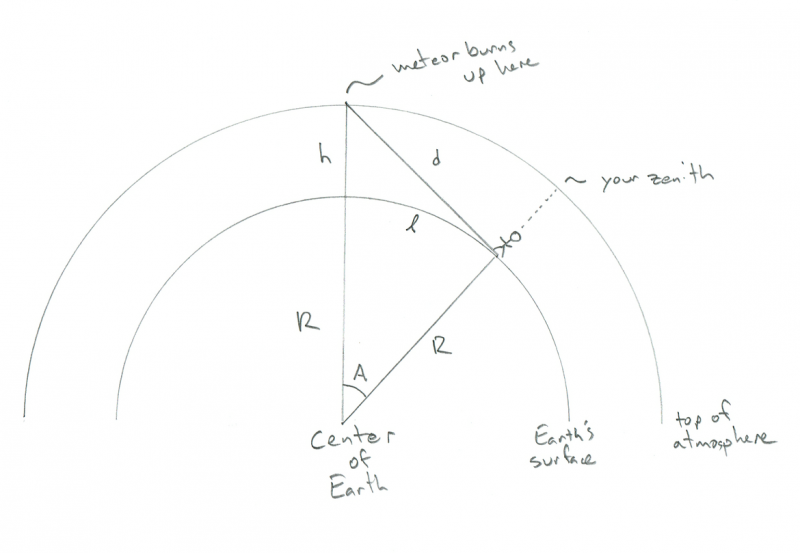
Shēma, kas parāda novērotāja ģeometriju, vērojot meteoru. Kredīts: Fils Plaits
Jūs varat redzēt mazo nūjiņu, kas stāv uz izliektas Zemes virsmas - pieņemsim, ka tas esat jūs - ar (arī izliektu) atmosfēru virs tām. Šajā diagrammā R ir Zemes rādiuss (6400 km), h ir meteora sadegšanas augstums (100 km), un d ir attālums no jums līdz meteoram. A ir leņķis starp jūsu stāvokli uz Zemes un meteora stāvokli virs tā, un kursīvais l (kā garumā) ir attālums, kas jums jānoiet, lai meteors atrastos tieši virs galvas (es zinu, ka tas šķiet dīvaini gribu zināt, bet izturieties ar mani). Dīvaini, jūs varat šeit aprēķināt visu, kas jums nepieciešams, nezinot d, bet c'mon, ir forši zināt, cik tālu ir meteors, vai ne?
Galvenais tam visam ir redzēt, ka leņķis starp meteoru, tevi un Zemes centru ir taisns leņķis. Tas ir tāpēc, ka meteors atrodas pie horizonta, kā jūs redzat (vai, ja vēlaties izklaidējošu žargonu, pieskaras līnijai iekšējā aplī, kur R to krusto). Tas padara trīsstūri par taisnu trijstūri, un, ja atceraties savu vidusskolas matemātiku, tas nozīmē, ka varat atrast visas malas un leņķus!
Atcerieties Pitagora teorēma ? Taisnstūra trīsstūrī hipotenūzas garuma kvadrāts ir vienāds ar pārējo divu malu kvadrātu summu*. Mūsu trīsstūrī hipotenūza ir R+h, bet pārējās malas ir R un d.
Tātad
(R+h)2= d2+ R.2
vai, reizinot kreiso pusi (izmantojiet FOLIJA ):
R2+ 2Rh + h2 = d2+ R.2
Atrisiniet d, lai redzētu, cik tālu meteors atrodas no jums. Ņemiet vērā, ka R2 ir abās pusēs, tāpēc atceliet tos, lai iegūtu
d2= 2Rh + h2
Vai
d = kvadrātsakne (2Rh + h2)
Nu, mēs zinām visus šos skaitļus! Plug-n-chug, mazulis:
d = kvadrātsakne (2 x 6400 x 100 + 10 000) = 1136 km
Aha! Tas nozīmē, ka, ja pie horizonta redzat meteoru, tas atrodas vairāk nekā 1100 kilometru attālumā! Tas ir tāls ceļš, un tehniski vistālāk no zemes var redzēt meteoru.
Tagad atradīsim kursīvo l. Vispirms mums jāzina leņķis A. Tam nepieciešama zināma trigonometrija. Tur ir daudz trig identitātes Jūs varat izmantot, lai to izdomātu, bet mans mīļākais†ir tas, ka taisnā trīsstūrī leņķa sinuss ir pretējās malas garums, dalīts ar hipotenūzes garumu. Tātad, ja mēs iegūstam šo attiecību, leņķa iegūšanai varam izmantot apgriezto sinusu (vai arkinsīnu).
sin (A) = d / (R + h)
tātad
A = bez-1(d / R + h)
Plug-n-chug atkal, un man A = 10 °. Tā ir pienācīga Zemes virsmas daļa!
Un tagad mēs varam iegūt kursīvu l. Ap Zemi ir 360 °, un Zemes apkārtmērs ir 2 x pi x rādiuss = 40 192 km, tātad
40 192 km / 360 ° = 112 kilometri uz grādu
kas savukārt nozīmē 10 ° = 1120 kilometrus. Tas ir diezgan tuvu d, kas nav pārāk pārsteidzoši. Zīmējumi ir pārspīlēti, bet patiesībā gaisa apvalks virs mums ir mazs, salīdzinot ar Zemes lielumu. Ja es rasējumus izveidotu pēc mēroga, jūs redzētu, ka d un l patiešām ir diezgan tuvu.
Labi, tad kāpēc es esmu karsts un nemierīgs, lai atrastu l? Sākotnējā jautājuma dēļ! Ja pēc šīs matemātikas esat aizmirsis, cik tālu var atrasties divi cilvēki un joprojām redzēt vienu un to pašu meteoru?
Tādā gadījumā meteors būtu tieši starp tiem un katrā attiecīgajā horizontā. Ģeometrija izskatās šādi:
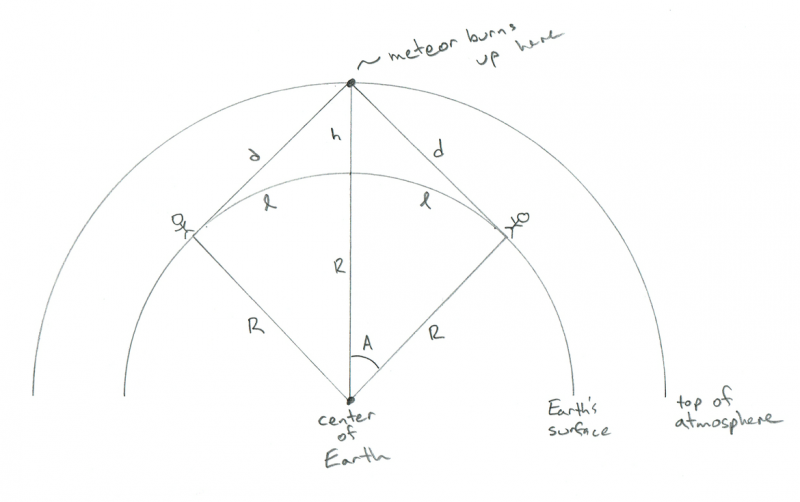
Shēma, kas parāda divu novērotāju ģeometriju, vērojot meteoru, kas sadeg tieši starp tiem. Kredīts: Fils Plaits
AHA! Tagad jūs redzat, kāpēc es gribu! Attālums starp diviem cilvēkiem ir tikai 2 x l! Tātad, tagad mums ir atbilde:
meitene zirnekļa tīkla vecāku ceļvedī
Lai divi cilvēki redzētu vienu un to pašu meteoru, viens no otra var atrasties ne vairāk kā 2 x 1120 = 2240 kilometru attālumā. Piemēram, tas ir diezgan tuvu attālumam starp Vašingtonu, DC un Denveru. Oho.
Starp citu, lai mainītu perspektīvu (burtiski), tas nozīmē, ka no meteora viedokļa tas var redzēt 2240 kilometrus platu Zemes gabalu (piemēram, DC Zemes austrumu daļā un Denveru rietumu daļā). Tas ir diezgan forši.
Un tas noved pie faktiskās atbildes uz Dīna jautājumu: ja viņš būtu 1000 km attālumā no savas ģimenes, tad jā, tehniski viņi varētu redzēt to pašu meteoru. Kā būtu ar to?
Tagad atkal tiek pieņemts, ka gaiss ir pilnīgi skaidrs un tas viss, kas patiesībā būtībā nav iespējams. Tātad šī matemātika attēlo ideālu situāciju (ieskaitot domu, ka meteors atrodas tieši starp tām).
Būsim reālistiskāki. Pieņemsim, ka meteors deg debesīs 45 ° augstumā virs horizonta abiem novērotājiem. Cik tālu viņi būtu viens no otra? Atkal, pieņemot, ka meteors atrodas tieši starp tiem, ģeometrija ir vairāk šāda:
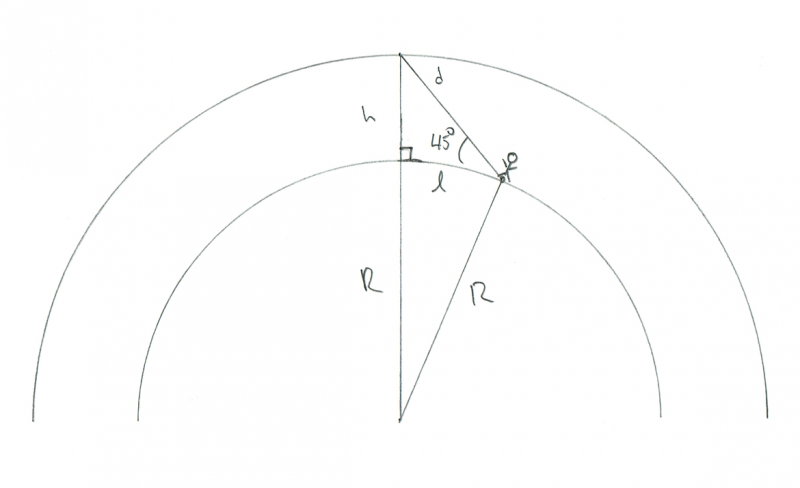
Shēma, kas parāda novērotāja ģeometriju, vērojot meteoru, kas deg 45 ° virs horizonta. Kredīts: Fils Plaits
To patiesībā ir grūtāk atrisināt, bet es zinu vēl vienu triku: ja pieņemam, ka l ir mazs, tad Zemes izliekumam nebūs nozīmes. Piemēram, ja es vēlos uzzināt attālumu starp diviem kokiem manā pagalmā, man vienalga, ka Zeme ir izliekta. Tik nelielā attālumā es varu pieņemt, ka tas ir plakans. Izteiksim šo pieņēmumu šeit.
Tādā gadījumā mums ir vēl viens taisnstūris, bet šoreiz taisnais leņķis ir zem meteora. Es to pat marķēju diagrammā ar nelielu kvadrātveida apzīmējumu. Tātad, ja tas ir 90 ° leņķis un mūsu leņķis pret meteoru ir 45 °, tad pēdējais leņķis (no meteora līdz novērotājam) ir arī 45 °. Tas nozīmē, ka tam jābūt vienādsānu trīsstūrim, tāpēc l un h ir vienādi! Tā kā mēs zinām, ka h ir 100 km, tad arī l.
Un tas nozīmē, ka attālums starp abiem mūsu novērotājiem ir divreiz lielāks jeb 200 km.
Starp citu, šajā gadījumā attālums līdz meteoram ir aptuveni 141 km. To es apstiprināšu kā vingrinājumu lasītājam.
Principā tas nozīmē, ka, ja jūs zināt, cik augstu no horizonta atrodas meteors, un augstumu, kādā tas dega, varat aprēķināt tā attālumu (vai, ja zināt attālumu, varat iegūt tā augstumu). Tomēr tas ir diezgan sarežģīts, un es domāju, ka šodien jums esmu uzmetis pietiekami daudz matemātikas.
Bet ir forši domāt, ka mazliet vidusskolas matemātikai var būt tik jautra pielietošana. Un es atzīstu, ka ir poētiski un romantiski zināt, ka, kamēr šķiršanās nav pārāk tālu, ir iespējams dalīties redzošās zvaigznes redzēšanā ar kādu citu. Cik jauka doma.
* In Oza zemes burvis , putnubiedēklis ir kļūdījies pēc viņam bija smadzenes.
† No protams Man ir mīļākā trig identitāte. Kas ir jūsu?













